検定・推定
1. 検定(仮説検定)
ある集団から抽出したサンプル(標本)の、統計量に関する仮説が正しいかどうか、統計学的に判定すること。
統計量・母数には、計量値(寸法・電気特性など)と計数値(故障率・不適合数など)がある。
(1) 仮説
たとえば2つの異なる母集団から抽出した統計量について、「両者の平均値に差がある/ない」・「両者のばらつきに差がある/ない」など、統計学に基づく2つの仮説を立てる。
① 帰無仮説H0:最終的に棄却されるべき仮説。
② 対立仮説H1:帰無仮説と対立する仮説。最終的に採択されるべき仮説。
もし、「両者が異なる特性を持つ」ということを示したい場合に、平均値をその根拠にするのであれば、「両者の平均値に差がない」を帰無仮説とし、「両者の平均値に差がある」を対立仮説とする。
(2) 分布と棄却域の設定
検定の結果が帰無仮説による統計量の分布のどこに属するかで、仮説の採択・棄却を判定するが、この判定に用いる分布形と棄却域を選択する。
分布形の種類
|
検定 |
目的 |
分布形 |
|
u検定 |
平均値(母標準偏差既知) 比率 |
標準正規分布 |
|
t検定 |
平均値(母標準偏差未知) |
t分布 |
|
χ2検定 |
ばらつき(母標準偏差既知) |
χ2分布 |
|
F検定 |
ばらつき(母標準偏差未知) |
F分布 |
その判定の基準となる有意水準(帰無仮説を棄却する確率)は、棄却域の設定によって決まる。通常は、5%か1%を使う。基準としては1%のほうがより厳しいので、5%では有意であっても、1%では有意では無い、ということも起こりうる。
単に両者が異なるか同じかを論じる場合には両側検定を、大小を論じる場合には片側検定を行う。
たとえば、有意水準5%の時に、両側検定では分布の両端でそれぞれ2.5%ずつ棄却域を設定し、片側検定では分布の上端・下端どちらかで5%の棄却域を設定する。
分布表には、累積分布関数の値が示されており、判定にはこの値を用いる。累積密度関数は、確率密度関数を積分したものである。
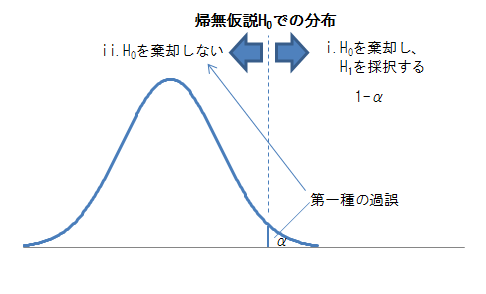
(3) 判定
判定は2通りで、仮にα = 5% の時には、
i. 有意水準5%で、帰無仮説H0を棄却し、対立仮説H1を採択した場合には、その信頼度は95%である。「5%有意である」とする。
標本の統計量が、帰無仮説による分布の5%の棄却域に入った場合に、そのように判定する。
第一種の過誤を犯す(間違えて本来正しいはずの帰無仮説H0を棄却してしまう)可能性(危険率)は5%である。
ii. 有意水準5%で、帰無仮説H0を採択し、対立仮説H1を棄却した場合には、帰無仮説を棄却するほどの根拠がないと考える。「5%有意でない」とする。積極的に帰無仮説が正しいという意味では無い。
標本の統計量が、帰無仮説による分布の5%の棄却域に入らなかった場合に、そのように判定する。
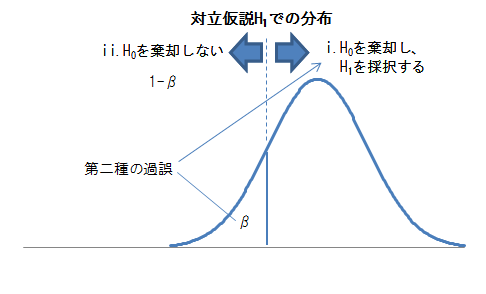
第二種の過誤を犯す(間違えて本来誤りのはずの帰無仮説H0を採択してしまう)可能性が何%なのかは、対立仮説による分布が一つに決まらないので、論じられない。
第一種の過誤を犯す確率(有意水準)をα とすれば、信頼率は、1-αである。
第二種の過誤を犯す確率をβとすれば、検出力は1-βとなる。
検出力1-βが低くなるのは、
① 母集団の分布が近い場合。
② 標本の数が少ない場合。
③ 有意水準の設定が低くて、厳しすぎる場合。
|
|
判定 |
|
|
i.H0を棄却し、 H1を採択する |
ii.H0を棄却しない
|
|
|
H0が誤りである場合に |
正しい判定 1-α |
第二種の過誤 β |
|
H0が正しい場合に |
第一種の過誤 α |
正しい判定 1-β |
2. 推定
検定の結果を受けて、サンプルが属する母集団の母数を、統計学的に推測すること。
母数にも、計量値と計数値がある。
(1) 点推定
サンプルの統計量を、母集団を表す母数として推定する。
(2) 区間推定
点推定で得られた母数の信頼区間を示す。
推定には、検定を用いた分布形を使う。
信頼区間の基準には、信頼度95%の区間推定と、信頼度99%の区間推定が、通常は使われる。
信頼区間と、検定における棄却域とは、全く別のものとして考える。
3. サンプリングと分布の規格化(規準化)
(1) 母数と統計量
推定では、統計量から母数を推定する。
|
|
母数 |
統計量 |
|
平均 |
|
|
|
不偏分散 |
|
|
|
標準偏差 |
|
|
(2) 母数の平均値μと標準偏差σによる規格化
正規母集団N(μ ,σ2) に属する統計量xは、正規分布N(μ ,σ2) に従う。
ここで新たに、規格化した統計量を
![]()
と定義した場合、統計量u0は、標準正規分布N(0 ,12) に従う。
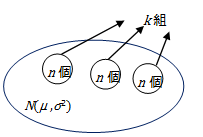
(3) サンプリングの規格化
正規母集団N(μ ,σ2)
から、ランダムにn個k組のサンプルを採り、n個の平均値を![]() とし、規格化した統計量を
とし、規格化した統計量を
![]()
と定義した場合、データ総数k個である統計量uは、標準正規分布N(0 ,12) に従う。
(4) 全ての統計量xの分布と、平均値![]() の分布のちがい
の分布のちがい
仮に、正規母集団N(μ ,σ2)のサンプル総数がnk個とした場合に、
A) n個ずつk組をサンプリングしたとき、
① データ総数nk個のxの分布はN(μ ,σ2)に従い、nk個のu0の分布はN(0 ,12)に従う。
② データ総数k個の![]() の分布はN(μ ,σ2/n)に従い、k個のuの分布はN(0 ,12)に従う。
の分布はN(μ ,σ2/n)に従い、k個のuの分布はN(0 ,12)に従う。
B) n個の1組をサンプリングしたとき、
① データ総数n個のxの分布はN(μ ,σ2)に従い、n個のu0の分布はN(0 ,12)に従う。
② データ総数1個の![]() はN(μ ,σ2/n)に従い、1個のuはN(0 ,12)に従う。
はN(μ ,σ2/n)に従い、1個のuはN(0 ,12)に従う。
4. 計量値の検定・推定
(1) u検定:平均値の検定(母集団の標準偏差σ0が既知の場合)
※ ただし、母集団の分布は正規分布に従うこと。
例:平均値を根拠に、従来品と新製品の特性に差があるといえるか
(新製品の母集団の標準偏差は、従来品の母集団の標準偏差と等しいものとする)
<検定>
① 仮説を立てる
帰無仮説H0:![]() 平均値に差があるといえない
平均値に差があるといえない
対立仮説H1:![]() 平均値に差があるといえる
平均値に差があるといえる
② 統計量として、新製品の特性の平均値 ![]() および、規格化したuを求める。
および、規格化したuを求める。
![]()
uは、標準正規分布に従う。
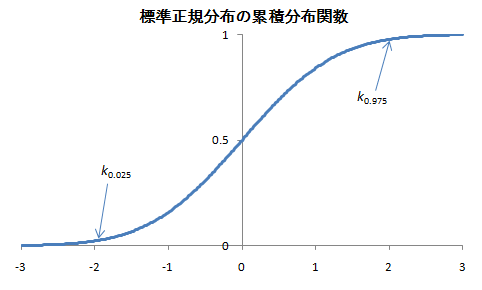
③ 判定
検定基準:標準正規分布表などから、値を読み取る。
・ 片側検定(5%,1%): ![]()
たとえば、両側検定5%(両端2.5%ずつ)の値1.960を採用すると、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 平均値に差があるといえる。
平均値に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 平均値に差があるといえない。
平均値に差があるといえない。
<推定>
新製品の母平均μを推定する
④ 点推定
![]()
⑤ 区間推定(信頼度95%)
信頼度(95%,99%):![]()
たとえば95%では、
![]()
![]()
平均値μは、95%の確率で、この区間に入る。
区間の中心は点推定の値になるので、次のように表現する場合もある。
![]()
(2) t検定:平均値の検定(母集団の標準偏差σ0が未知の場合)
※ ただし、母集団の分布は正規分布に従うこと。
例:平均値を根拠に、従来品と新製品の特性に差があるといえるか
(新製品の母集団の標準偏差は、従来品の母集団の標準偏差と異なるものとし、サンプルの不偏分散の平方根![]() を母数の標準偏差の推定値として採用する)
を母数の標準偏差の推定値として採用する)
<検定>
① 仮説を立てる
帰無仮説H0:![]() 平均値に差があるといえない
平均値に差があるといえない
対立仮説H1:![]() 平均値に差があるといえる
平均値に差があるといえる
② 統計量として、新製品の特性の平均値 ![]() および、規格化したtを求める。
および、規格化したtを求める。
![]()
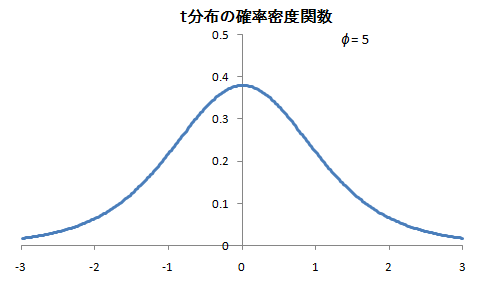
t は、自由度![]() のt分布に従う。
のt分布に従う。
なお、t分布は、![]() の時に標準正規分布と等しくなる。
の時に標準正規分布と等しくなる。
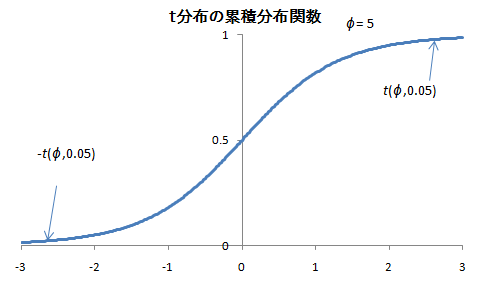
③ 判定
検定基準:t分布表などから、値を読み取る。
・ 両側検定(5%,1%):![]()
・ 片側検定(5%,1%):![]()
たとえば、両側検定5%では、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 平均値に差があるといえる。
平均値に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 平均値に差があるといえない。
平均値に差があるといえない。
<推定>
新製品の母平均μを推定する
④ 点推定
![]()
⑤ 区間推定
信頼度(95%,99%): ![]()
たとえば95%では、
![]()
![]()
平均値μは、95%の確率で、この区間に入る。
(3) χ2検定:ばらつきの検定(母集団の標準偏差σ0が既知の場合)
さらに、母集団の平均値が既知か未知かで検定に用いる分布の式が若干異なるが、実際ばらつきの検定をする前に、平均値が既知であるようなケースはほとんどないと考えられるので、ここでは平均値は未知として進める。
※ ただし、母集団の分布は正規分布に従うこと。
例:標準偏差を根拠に、従来品と新製品のばらつきに差があるといえるか
(基準となる従来品の母集団の標準偏差がわかっているものとする)
<検定>
① 仮説を立てる
帰無仮説H0:![]() 標準偏差に差があるといえない
標準偏差に差があるといえない
対立仮説H1:![]() 標準偏差に差があるといえる
標準偏差に差があるといえる
② 統計量として、新製品の特性の平均値 ![]() 、偏差平方和S、不偏分散Vを規格化したχ2を求める。
、偏差平方和S、不偏分散Vを規格化したχ2を求める。
![]()
![]()
![]()
χ2
は、自由度![]() のχ2(カイ2乗)分布に従う。
のχ2(カイ2乗)分布に従う。
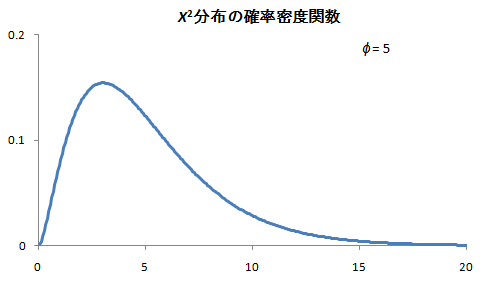
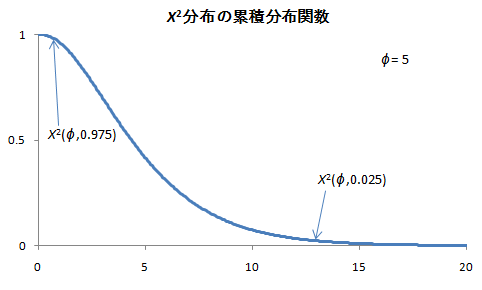
③ 判定
検定基準:χ2分布表などから、値を読み取る。
・ 両側検定(5%,1%): ![]()
・ 片側検定の下側(5%,1%): ![]()
・ 片側検定の上側(5%,1%): ![]()
たとえば、両側検定5%では、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 標準偏差に差があるといえる。
標準偏差に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 標準偏差に差があるといえない。
標準偏差に差があるといえない。
<推定>
新製品の母平均σを推定する
④ 点推定
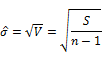
⑤ 区間推定
信頼度(95%,99%): ![]()
たとえば95%では、
![]()
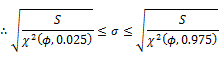
標準偏差σは、95%の確率で、この区間に入る。
(4) F検定:ばらつきの検定(母集団の標準偏差σ0が未知の場合)
※ ただし、母集団の分布は正規分布に従うこと。
例:標準偏差を根拠に、新製品1と新製品2のばらつきに差があるといえるか
(両者の母集団の標準偏差はわからないものとする)
<検定>
① 仮説を立てる
帰無仮説H0:![]() 標準偏差に差があるといえない
標準偏差に差があるといえない
対立仮説H1:![]() 標準偏差に差があるといえる
標準偏差に差があるといえる
② 統計量として、両者の特性の平均値 ![]() 、偏差平方和S、不偏分散Vの比を表すFを求める。
、偏差平方和S、不偏分散Vの比を表すFを求める。
![]()
![]()
![]()
![]()
![]()
![]()
F は、自由度![]() のF分布に従う(等分散検定)。
のF分布に従う(等分散検定)。
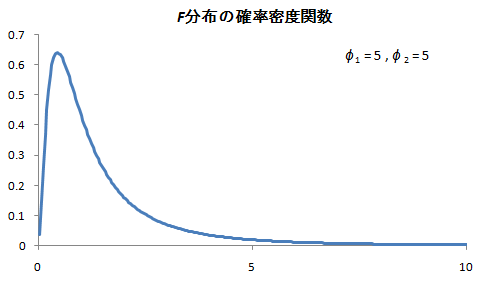
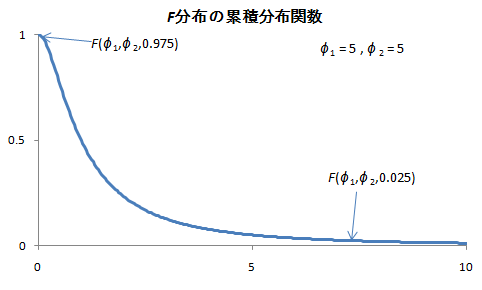
③ 判定
検定基準:F分布表などから、値を読み取る。
・ 検定(5%,1%):![]()
あらかじめ、 ![]() という条件を付加したので、上側のみ示した。
という条件を付加したので、上側のみ示した。
一般に、次式が成り立つ。
![]()
たとえば、有意水準5%の検定では、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 標準偏差に差があるといえる。
標準偏差に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 標準偏差に差があるといえない。
標準偏差に差があるといえない。
<推定>
分散比Fを推定する
④ 点推定
![]()
⑤ 区間推定
信頼度(95%): ![]()
![]()
分散比Fは、95%の確率で、この区間に入る。
5. 2組の計量値の差の検定・推定
(1) t検定:平均値の差の検定(2組のデータに対応が無く、独立である場合)
※ 母集団の分布は正規分布に従うこと。
※ あらかじめF検定を行い、両者が等分散であること。
例:平均値の差を根拠に、新製品1と新製品2の特性に差があるといえるか
<検定>
① 新製品1と新製品2にF検定を行い、両者が等分散であることを確かめる。
② 仮説を立てる
帰無仮説H0:![]() 平均値に差があるといえない
平均値に差があるといえない
対立仮説H1:![]() 平均値に差があるといえる
平均値に差があるといえる
③ 統計量として、両者の特性の平均値 ![]() および、新たに定義した分散V 、規格化したtを求める。
および、新たに定義した分散V 、規格化したtを求める。
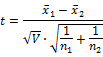
![]()
![]()
![]()
t は、自由度![]() のt分布に従う。
のt分布に従う。
④ 判定
検定基準:t分布表などから、値を読み取る。
・ 両側検定(5%,1%):![]()
・ 片側検定(5%,1%):![]()
たとえば、両側検定5%では、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 平均値に差があるといえる。
平均値に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 平均値に差があるといえない。
平均値に差があるといえない。
<推定>
新製品の母平均の差![]() を推定する
を推定する
⑤ 点推定
![]()
⑥ 区間推定
信頼度(95%,99%): ![]()
たとえば95%では、
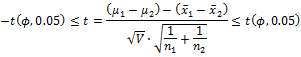
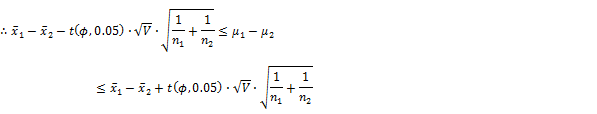
母平均の差![]() は、95%の確率で、この区間に入る。
は、95%の確率で、この区間に入る。
(2) t検定:特性の差の検定(2組のデータに対応がある場合)
※ 母集団の分布は正規分布に従うこと。
例:ある製品の特性を測定した場合に、測定器1と測定器2の測定値に差があるといえるか
<検定>
① 仮説を立てる
![]()
帰無仮説H0:![]() 測定値に差があるといえない
測定値に差があるといえない
対立仮説H1:![]() 測定値に差があるといえる
測定値に差があるといえる
② 統計量として、測定値の差dの平均値 ![]() および、分散V 、規格化したtを求める。nは測定の回数ではなく、サンプル数をそのまま使う。
および、分散V 、規格化したtを求める。nは測定の回数ではなく、サンプル数をそのまま使う。
![]()
![]()
![]()
t は、自由度![]() のt分布に従う。
のt分布に従う。
③ 判定
検定基準:t分布表などから、値を読み取る。
・ 両側検定(5%,1%):![]()
・ 片側検定(5%,1%):![]()
たとえば、両側検定5%では、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 測定値に差があるといえる。
測定値に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 測定値に差があるといえない。
測定値に差があるといえない。
<推定>
測定値の差dを推定する
④ 点推定
![]()
⑤ 区間推定
信頼度(95%,99%): ![]()
たとえば95%では、
![]()
測定値の差dは、95%の確率で、この区間に入る。
6. 計数値の検定・推定
中心極限定理から、どんな分布でも、サンプル数nが十分大きければ、標本平均の分布は、正規分布に従う。
二項分布B(n,p)について考えると、![]() で正規分布
で正規分布![]() に近づく(ラプラスの定理)。
に近づく(ラプラスの定理)。
ここで、前述の、計量値の正規分布と比較して考える。
![]()
計数値である不適合品個数x や不適合品率p に関しても同様の式が成り立ち、
![]()
![]()
と定義すると、u0は近似的に標準正規分布N(0,12)に従う。
(ただし、近似条件:![]() かつ
かつ![]() )
)
推定においては、標本比率から母比率を推定する。
(1) 正規近似法-u検定:比率の差の検定(母比率P0が既知の場合)
例:不適合品率の差を根拠に、従来工程と新工程の工程能力に差があるといえるか
<検定>
① 仮説を立てる
帰無仮説H0:![]() 不適合品率に差があるといえない
不適合品率に差があるといえない
対立仮説H1:![]() 不適合品率に差があるといえる
不適合品率に差があるといえる
② 統計量として、新工程の不適合品率pおよび、規格化したu0を求める。
![]()
u0は、標準正規分布に従う。
③ 判定
検定基準:標準正規分布表などから、値を読み取る。
・ 両側検定(5%,1%): ![]()
・ 片側検定(5%,1%): ![]()
たとえば、両側検定5%(両端2.5%ずつ)の値1.960を採用すると、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 不適合品率に差があるといえる。
不適合品率に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 不適合品率に差があるといえない。
不適合品率に差があるといえない。
<推定>
新工程の母不適合品率Pを推定する
④ 点推定
![]()
⑤ 区間推定(信頼度95%)
信頼度(95%,99%):![]()
たとえば95%では、
![]()

Pは、95%の確率で、この区間に入る。
(2) 正規近似法-u検定:2組の比率の差の検定(母比率Pが未知の場合)
例:不適合品率の差を根拠に、新工程1と新工程2の工程能力に差があるといえるか
<検定>
① 仮説を立てる
帰無仮説H0:![]() 不適合品率に差があるといえない
不適合品率に差があるといえない
対立仮説H1:![]() 不適合品率に差があるといえる
不適合品率に差があるといえる
② 統計量として、新工程の不適合品率pおよび、規格化したu0を求める。
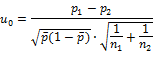
![]()
u0は、標準正規分布に従う。
③ 判定
検定基準:標準正規分布表などから、値を読み取る。
・ 両側検定(5%,1%): ![]()
・ 片側検定(5%,1%): ![]()
たとえば、両側検定5%(両端2.5%ずつ)の値1.960を採用すると、
i. ![]() ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
ならば帰無仮説H0は棄却され、対立仮説H1が採択される。有意水準5%にて有意差あり。
![]() 不適合品率に差があるといえる。
不適合品率に差があるといえる。
ii. ![]() ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
ならば帰無仮説H0は棄却されない。有意水準5%にて有意でない。
![]() 不適合品率に差があるといえない。
不適合品率に差があるといえない。
<推定>
母不適合品率の差を推定する
④ 点推定
![]()
⑤ 区間推定(信頼度95%)
信頼度(95%,99%):![]()
たとえば95%では、
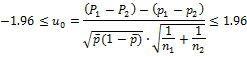
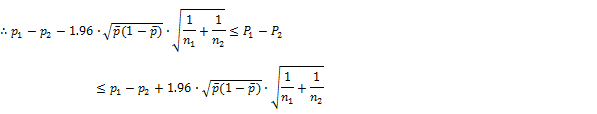
![]() は、95%の確率で、この区間に入る。
は、95%の確率で、この区間に入る。